Power vs. Torque (Pt. 1): Why Nobody Knows What the Hell Torque is

Introduction:

“Power determines how fast you are going when you hit the wall. Torque determines how much of the wall you take with you.”

The above quote is a common refrain heard throughout the automotive community; typically used as a colloquial attempt to explain (I guess?) the difference between the power and torque of an engine. The first problem with this quote is that most of the people who use it could not coherently define the two terms separately if asked. Second, the quote doesn’t actually tell us anything useful or accurate about torque. It’s also pretty vague about power.

A more accurate quote might read:

“Power, load transfer, tire grip, vehicle mass, aerodynamics, and gearing all help to determine how fast you are going when you hit the wall. Vehicle mass and speed at impact (momentum) determine how much of the wall you take with you.”

(Note that engine torque does not appear in the above quotation)

Alright so now that I’m done being a smartass, let me begin to explain. The goal of this post will be to define and explain the differences between power and torque as they apply to a vehicle system. There seems to be an enormous lack of clarity in the automotive community at large about these two terms and what they mean. Manufacturers publish their top-line power and torque numbers without context, and automotive media and enthusiasts alike blindly parrot these numbers as if they are both all-important in and of themselves. This blog will be largely dedicated to taking down the many misconceptions in the automotive community, and the power/torque brouhaha is my first target.

First and foremost, we have to define the terms power and torque. I know that much of the following table-setting might come off as a bit pedantic, but it will help to explain these concepts with context so that they can be clearly and fully understood. Using some (simple, I promise) engineering math I am going to explain the actual difference between the two; or more accurately, how they are inextricably related. By subtly shifting the way you think about how to interpret what these equations are actually telling us, I will explain both power and torque in an intuitive way that hopefully everybody can understand.

Thinking in Terms of Units:

Before I get to the respective definitions, I wanted to briefly share a mental technique that I think (if taken seriously) will help a lot in understanding this and many other engineering concepts: Paying attention to and understanding the "units" in an equation.

Working in various industries over the years, I have found it extremely helpful to decrypt confusing concepts by taking an explicit look at the units involved in the relevant equations. It can also help you to quickly identify mistakes when calculating numbers. To take a very simple example of the former, let's look at the equation for speed (v);

$ v = \frac{x}{t} $

Where x is the distance (units of feet, ft) traveled of the object in question, and t is the time elapsed (units of seconds, sec).

So, if you punt a Boston Terrier and he travels 8 feet in the span of one second, then his speed over that time would be:

$ v = \frac{8 ft}{1 s} = 8 \frac{ft}{s} $.

So, thinking in terms of the units, we could just look at the units: feet per second. This framing gives us an intuitive clue about what the equation is telling us. How many feet in how many seconds the object is traveling. Pretty straight-forward. The relevant information is captured in the units alone. So, how can we use this to understand power and torque?

Defining Power:

Coming back to the topic at hand; if you look at the units for power (P) and think about it a little bit, you may notice something interesting;

$ P = \frac{lb-ft}{sec} $

Contained right in the units are two huge clues. Do you remember what else is measured in lb-ft? You may have (correctly) identified torque. But it is also the units for energy (or N-m for you metric perverts out there). What the units are telling us here is that power, properly defined, is a measure of the energy produced (or consumed) by the system in question over a given period of time. In other words, power is the rate of energy production or consumption.

... power, properly defined, is a measure of the energy produced (or consumed) by the system in question over a given period of time. In other words, power is the rate of energy production or consumption.

For a car traveling along a road at constant engine power output, you are using the engine to add energy to the vehicle. This could be to add kinetic energy (accelerate), or to add potential energy (climb a hill), or to add energy to overcome the various losses involved with speeding down a road (aerodynamic drag, tire deformation, gearbox losses, etc…). The more power your engine is delivering, the more energy you are putting into the system over a given amount of time.

Follow me so far? If so, your next question might be: “So then how does torque factor into all of this? Clearly it must be an important number that matters a lot since manufacturers go to great lengths to emphasize the torque numbers for their engines. Right?”

Ehh… Not really… At least not for overall system performance.

Allow me to explain.

Defining Torque:

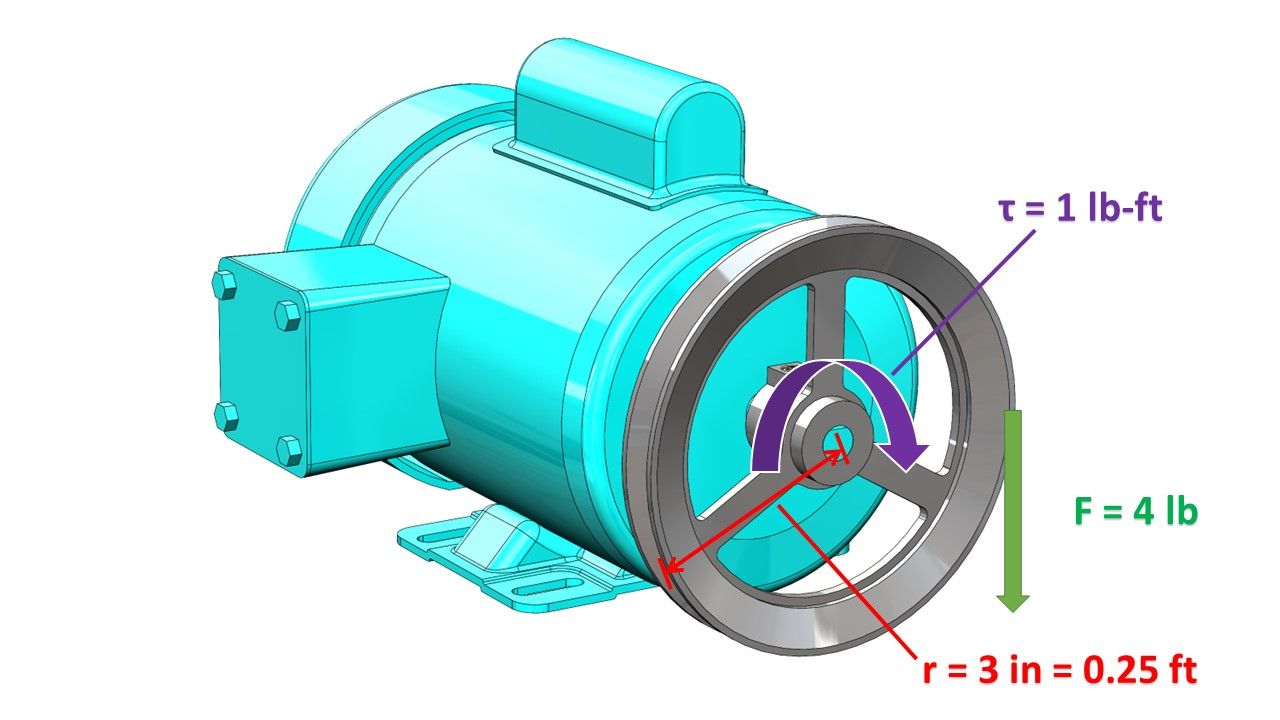
First off, an elementary definition of torque is in order. Torque is simply a force applied at a certain distance (sometimes called the “moment arm”) from the center of rotation. The equation for torque ($\tau$) is:

$ \tau = F \cdot r $

Where F is an applied force (units of lb), and r is the moment arm (units of ft) at which the force is applied (r is a radius if applied to a circular wheel).

Torque is simply a force applied at a certain distance (sometimes called the “moment arm”) from the center of rotation.

For example, let’s say we have an electric motor which is applying a constant torque of 1 lb-ft to the shaft by using its witchcraft and magic magnets. If we put a pulley on the shaft with an outside diameter of 6 inches (radius of 3 inches, 0.25 ft), then we can calculate the applied force on the outside of the pulley (assuming a static system here) as:

$ F = \frac{\tau}{r} = \frac{1 lb-ft}{0.25 ft} = 4 lb $

Make sense? Okay, so how does this information tie into a vehicle with an engine that makes both power and torque?

How Power and Torque are Related:

Alright, now let’s go back to some more simple engineering math by looking at the equation that is used to calculate power of an engine. Assume we have an engine with the crankshaft or flywheel attached directly to a dynamometer (dyno). A dyno directly measures only two things: the crankshaft rotational speed (rev/min, rpm) and the torque being generated by the engine at a given point in time. Exactly how is a topic for a different day, so for now just trust me on this one. Once the torque at a given engine speed is known, a computer calculates and displays the engine power using the following equation;

$ P = \frac{\tau_\text{eng} \cdot \omega_\text{eng}}{5,252} $

Where P is the calculated Power (horsepower), $\tau$ is Torque (lb-ft), and $\omega$ is the Engine rotational speed (rev/min).

Since we are using horsepower instead of lb-ft/sec, and rev/min instead of radians per second, the 5,252 is the relevant conversion factor to get from one to the other.

What becomes obvious right away is that engine power is DIRECTLY related to engine torque. The torque value is just one input into the equation for power. The other half of what matters here is the engine speed.

AHA! So surely an engine that makes more torque will make more power then, right??? So torque DOES matter! Right?

Again, ultimately no...

Why Torque Doesn't Matter: Let's Piss Off Some Diesel Bros

I finally figured this part out when I was working in heavy industry and designing machines that use gearmotors. A gearmotor is simply an electric motor coupled to a gearbox (see picture below for clarity).

One interesting thing that I eventually keyed in on is that the way these things are made is that they are 100% modular, where a single motor design can be mated to literally hundreds of different gearboxes depending on the desired gear ratio and resultant shaft output speed. A particular manufacturer might list options for a 1 hp motor with options for a maximum output shaft speed of anything from 0.19 rpm (yes, seriously) to 1,100 rpm. The gearbox with the 0.19 rpm output will have a MUCH higher output shaft torque (bigger gearbox, larger output shaft, etc.) than the 1,100 rpm output version. However, they are both achieving this with the same power. How is this possible?

Well if we remember back to our equation for power, we can once again recall that the power and torque are DIRECTLY related. Or to put it another way, the output torque can be calculated solely using the power, speed (input or output), and gearbox ratio; no knowledge of the input torque is directly required.

For an automobile, what matters most for determining the acceleration and top speed of the vehicle is power and gearing (assuming equivalent aerodynamics, a subject for a different post). Take, for example, two drastically different engines with much different torque characteristics; say, a high torque Diesel engine and a high revving (but lower peak torque) gas engine. Both of these engines, given the proper gearing, can achieve the same acceleration, top speed, towing capacity, etc, as long as both engines deliver the same amount of power.

So here is the top-level takeaway regarding power: The input torque can always be converted to whatever wheel torque is desired through gearing. The more power you are making, the more drive wheel torque you can make at a given vehicle speed. You read that right: For any given vehicle speed, peak engine torque is totally irrelevant. What you care about is how much power can be produced.

[SPOILER: Next month's post will be a supplement to this post where I perform public math to prove exactly the above hypothetical. So please withhold your vitriol and teeth-gnashing until you read next month’s installment.]

This, in a nutshell, is why power matters much more than a torque number for an automobile engine. If we were talking about a static system, rpm = 0 and power = 0, then torque would be the only relevant metric. To return to the gearmotor example; a 1 hp gearmotor could theoretically be configured to deliver 1,000 lb-ft of torque at a very low rotational speed. If you had all the time in the world, that might work for you. To speed this process up, you may wish to add power so that you could have the same amount of output shaft torque to handle your load, but at an elevated shaft speed.

Since an automobile is a moving system that needs to deliver drive wheel torque at elevated vehicle speed, power is the relevant factor.

So, why are so many people (including manufacturers) constantly touting torque numbers as all-important? The short answer is that the public largely doesn't understand the above relationship between torque and power. The slightly longer answer is explained in further detail below...

Why Some People Believe that Torque Matters:

Having thought about this a lot, this is why I believe that some people believe that torque matters;

When people subjectively refer to a “torque-y” motor, what they specifically mean is an engine that makes good low-end torque, which generally results in a higher, more impressive looking top-line peak torque number. Since horsepower always equals lb-ft of torque at 5,252 rpm (refer to the above equation for power) an engine can make impressive looking torque numbers low in the rev range (1,000-3,000 rpm). However, if the torque production drops off at higher revs the top-line power number may appear less impressive. Regardless, what a higher number for low-end torque translates to in the context of the above-described power/torque relationship is an engine that makes good low-end power. This is useful for a couple of reasons.

Historically, most vehicle platforms were configured using a manual transmission. The first relevant issue with a manual transmission is the clutch. When the vehicle is sitting at a standstill and the driver needs to accelerate, the engine’s crankshaft is constantly moving at an idle speed around 200-500 rpm while the transmission’s input shaft is stationary. To accelerate, the input shaft speed must accelerate to the engine speed. To do this with a manual transmission, the clutch must slip until the vehicle is moving fast enough so that the transmission input shaft speed is sufficiently high to not stall the engine.

The second problem with a manual transmission is the limited number of gears. One way to solve the above problem and minimize the amount of clutch slip is to use a very short first gear. However, this then necessitates a shorter second gear to ensure the rpm drop during shifting isn’t too extreme. If you only have 4-5 forward gears, this would be an inefficient use of the first couple of gears.

A common solution to this problem is for manufacturers to utilize an engine that makes good low-end power (low-end torque if you prefer). That way a manual transmission with a reasonable first gear ratio can be used, and the limited number of remaining gears is not as big of an issue. As a secondary benefit, good low-end power production allows good drivability at lower engine rpm’s, which typically results in less engine noise and vibrations when cruising around on the street. This is the reason why many “torque-y” engines are so popular and subjectively pleasing.

However, for modern automatic transmissions with torque converters (a mismatch between engine speed and transmission input shaft speed doesn’t matter as much) and gearboxes with many gears, this is much less of an issue. Think of the 10+ speed gearboxes offered by many manufacturers these days. This leads to the ability, to some extent, for manufacturers to feasibly utilize engine configurations with less low-end torque/power; I think it’s no coincidence that the modern 4-cylinder turbocharged engine has become so popular with manufacturers.

As you can see it very much depends on the application as to where in the rev range you want the engine to make power. If using an older manual gearbox; probably good low-end torque/power is best. For a modern automatic transmission and an engine that is well muffled, and where high power delivery is needed only for intermittent passing events, an engine making more power in the high rev range is just as useful. The overall point here is that it still doesn’t so much matter how much torque the engine is making at any given point: The only thing that matters is how much power you are making. That’s what is relevant for a moving vehicle.

Tying It All Together:

So, to wrap up: Engine power at low rotational speeds can be important to provide a good driving experience for street driving (depending on the transmission used). Particularly accelerating from a stop, which is why manufacturers tend to design engines with good low-end torque (and therefore good low-end power) characteristics. However, overall engine power is much more important for most situations which don't require accelerating from a complete stop, or if the speed mismatch between the crankshaft and the transmission input shaft can be sufficiently managed (automatic transmission witchery, or packing tons of gears into the transmission).

However, due to a lack of deep understanding of the concepts of power and torque, most people make far too big a deal about peak engine torque and treat it as some sort of all-important number. This is reinforced by manufacturers who lean into this phenomenon and choose to advertise their torque numbers as a "big-deal" number in and of itself. Mal-educated automotive journalists then perpetuate this ignorance by blindly publishing torque numbers, and making a big deal out of the torque number without considering other important factors; like the engine speed at which peak torque occurs, or whether the engine only makes good torque in one small area of the rev range.

The reality is that while high torque numbers may look impressive, they are pretty much irrelevant unless you understand the full context of the relationship between power and torque. It completely depends on where the torque is made, and what the gear ratios involved are. As long as a vehicle is properly geared, the number that really matters is power.

Pt. 3 of this post will delve into the details of engine design considerations and how they differ for a low-speed, high-torque engine (think a truck Diesel motor), compared to a high-speed, low-torque engine (think a sports car gas motor).

So, while power factors heavily in determining how fast you're going when you hit the wall, you now know that torque, by itself, has almost nothing to do with how much of the wall you will take with you. Thanks for reading!

If you found this post to be useful, or you want to send me love mail or hate mail, please feel free to provide feedback to mechanicalsuperiority@gmail.com